Analysis und Lineare Algebra (Mathematik 2) für Informatiker

Aktuelles

• Diese Seite ist in den Learning-Campus umgezogen!

•  MATERIALIEN zur Vorlesung.

Literatur

• [T] "Mathematik für Informatiker", Band 1 & 2 von Gerald und Susanne Teschl, Springer
• [W] "Konkrete Mathematik (nicht nur) für Informatiker", Edmund Weitz, Springer
• [JL] Videos von Jörn Loviscach (http://www.j3l7h.de/videos.html)
• Hinweis: Viele Bücher bekommen Sie als eBook kostenlos über die Hochschule:
• über OPAC im Netzwerk der Hochschule, von zu Hause über VPN
• auf der Springer-Verlag-Seite: "Log in" > "Log in via Shibboleth or Athens" > "find your institution (via Shibboleth)" > "Technische Hochschule Rosenheim"

Weitere Infos

Tipps zu den Lernmaterialien

• Der Ordner MATERIALIEN wird über die Hochschul-Cloud (LRZ Sync+Share) bereitgestellt.
• mit Ordner auf Festplatte synchronisieren: Windows-PC, Linux-PC, MAC
• Android (Google PlayStore), iOS (Apple App-Store)
• Info unter: https://www.fh-rosenheim.de/intranet/einrichtungen/rechenzentrum/it-services/zentrale-speichermoeglichkeiten/hochschul-cloud/
• Watch YouTube videos with higher speed

Inverted Classroom

• Inverted Classroom: 
• Inverted Classroom als moderne digitale Lehrmethode (auf YouTube) 3:09 
• https://de.wikipedia.org/wiki/Umgedrehter_Unterricht
• Workload-Berechnung nach Bologna (7 CP = 210h Arbeit):
• Präsenz: 6h/Woche (6h*15 = 90h)
• Selbststudium: 8h/Woche (8h*15 = 120h)

Weiterführende Empfehlungen

• Wolfram-α: Doku/Beispiele, Doku/Beispiele Maths
• OOP Tutorial: 2-dimensional Vector as Java Object 
• OOP Tutorial: 2-dimensional Vector as Scala Object 
• Tutorial: Determinant of a Matrix in Java
• Vorlesung OOP in Java mit YouTube Playlist
• MOOC: Introduction to Programming (Java) auf Udacity
• MOOC: Algorithmen und Datenstrukturen mit Java auf iversity

Beratung

• Beratung: Studiengang und übergreifend, soziale und psychologische Beratung

---

Vorlesung - Inhalt und Termine

Organisatorisches...
Komplexe Zahlen
1. Komplexe Zahlen	V1/2
Analysis
2. Folgen, Grenzwerte, Stetigkeit	V3/4
3. Grundlagen zu Ableitungen und Integralen	V5/6
4. Ableitung	V7
5. lokale Extrema, Wendepunkte	V8
6. lineare Näherung samt Anwendungen	V9
7. Integral	V10
8. Integrationsregeln	V11:
9. Schmiegeparabel, Taylor-Polynome	V12
10. Rest nach Taylor, Potenzreihen	V13
Lineare Algebra
11. Vektorräume	V14
12. Geradengleichung, Skalarprodukt	V15
13. Matrizen	V16
14. Lineare Gleichungssysteme, Rang, Kern	V17/18
15. Determinante, Spatprodukt, Vektorprodukt, inverse Matrix	V19/20
16. Cramer-, Gauss-, Jacobi-Verfahren	V21
17. Eigenvektoren	V22/23
18. Anwendung von EV: Google Page Rank	V24
Wiederholung und Klausurvorbereitung
Aufgaben zu Analysis und Lineare Algebra: Bitte vorab Themen wiederholen!
Probeklausur

---

Vorlesung 1/2 - Komplexe Zahlen

Vorlesung 1 (zwei Teile A und B!)
A. Zahlenbereiche (nur Komplexe Zahlen!) - Skript unter MATERIALIEN

1. optional (Wiederholung aus 1.Semester): Natürliche, ganze und rationale Zahlen 3:33
2. optional (Wiederholung aus 1.Semester): Reelle Zahlen 4:54
3. Komplexe Zahlen 6:49
4. Real- und Imaginärteil, Länge, Gaußsche Zahlenebene 6:51
5. Wozu komplexe Zahlen? 5:31
6. optional (Wiederholung aus 1.Semester): Rechenregeln, Assoziativität, Kommutativität, Distributivität 6:14
7. optional: Quaternionen, unendlich große Zahlen 4:16
8. optional (Wiederholung aus 1.Semester): 04.06 Intervalle reeller Zahlen 2:41
9. optional (Wiederholung aus 1.Semester): 04.07 Stellenwertsysteme, Binärsystem 8:51
10. optional (Wiederholung aus 1.Semester): 04.08 Exponentialschreibweise 5:50

B. imaginäre Einheit, Gaußsche Zahlenebene; Betrag, Winkel; komplexe Konjugation; Grundrechenarten für komplexe Zahlen - Skript unter MATERIALIEN

1. Gaußsche Zahlenebene, komplexe Zahlen 10:39
2. Betrag, Winkel einer komplexen Zahl 12:44
3. Addition, Subtraktion komplexer Zahlen 4:32
4. Multiplikation komplexer Zahlen 14:47
5. Division komplexer Zahlen 13:02
6. weiter Division komplexer Zahlen, Winkel bestimmen 2:36

Vorlesung 2
C. Potenzen und Wurzeln komplexer Zahlen; Eulersche Identität; Additionstheoreme; vollständige Faktorisierung von Polynomen - Skript unter MATERIALIEN

1. Ganzzahlige Potenzen und Wurzeln komplexer Zahlen 13:53
2. Wurzeln in Wolfram Alpha 1:46
3. weiter Wurzeln komplexer Zahlen 4:17
4. Eulersche Identität e^(ix)=cos(x)+isin(x) 11:42
5. weiter Eulersche Identität 12:51
6. sin, cos, Potenzreihen, Additionstheoreme 14:19
7. Polardarstellung, Multiplikation, Division, Potenz.avi 7:59
8. weiter Polardarstellung, Wurzel 7:39
9. Fundamentalsatz der Algebra, Nullstellen von Polynomen im Komplexen 14:50
10. weiter Fundamentalsatz der Algebra, Nullstellen von Polynomen im Komplexen 14:31

Ergänzungen (optional zum Üben und Vertiefen):

• Ordinalzahlen, Konstruktion von Zahlen nur aus der leeren Menge 13:32
• Mächtigkeit, 1. und 2. Cantorsches Diagonalverfahren, (Über-)Abzählbarkeit 25:46
• Beispiel für Multiplikation und Division komplexer Zahlen 8:44
• Warum i² gleich -1 sein muss 13:37
• Rechnen mit komplexen Zahlen, Multiplikation und Division 11:28
• Wurzel aus der imaginären Einheit 19:19
• quadratische Gleichung mit komplexwertigen Lösungen 4:23
• rationale Zahlen, periodische Dezimalbrüche, algebraische Gleichungen 16:34
• Fingerübungen mit komplexen Zahlen, Länge, Winkel; Potenzen; Wurzeln von i 13:39
• Die Werte von 1 durch (3+ix) bilden einen Kreis in der Gausschen Zahlenebene 16:10
• Multiplikation komplexer Zahlen algebraisch und geometrisch 15:52
• Division komplexer Zahlen algebraisch und geometrisch 18:38
• Eulersche Identität, Polardarstellung, Sinus hyperbolicus 36:09
• Multiplikation am Einheitskreis geometrisch, Länge, komplex Konjugiertes 26:35
• Gleichungen und pq-Formel mit komplexen Zahlen 11:10
• Zwei hoch die imaginäre Einheit i; imaginäre Einheit hoch die imaginäre Einheit 12:07
• dritte Wurzeln einer komplexen Zahl 14:17
• Gleichung mit komplexen Zahlen; Wurzel aus i 4:52
• quadratische Gleichung mit komplexen Zahlen 3:06
• Drehungen im R2 über komplexe Zahlen und Eulersche Identität 9:30
• Cosinus von i; Cosinus mit e hoch i phi schreiben 12:13
• Logarithmus einer komplexen Zahl 9:43
• komplexe Linearfaktoren eines Polynoms 6:19

---

Vorlesung 3/4 - Folgen, Grenzwerte, Stetigkeit

• Skript unter MATERIALIEN

Vorlesung 3:

1. Folgen 14:33
2. beschränkte, monotone Folgen 5:43
3. Konvergenz, bestimmte Divergenz 18:41
4. weiter Konvergenz, Grenzwert 11:30
5. Grenzwertsätze 11:35

Vorlesung 4:

1. Grenzwerte von Funktionen 15:29
2. Stetigkeit, stetig hebbare Definitionslücken 24:33
3. Regel von L'Hôpital, Null durch Null 14:10

Ergänzungen (optional zum Üben und Vertiefen):

• Grenzwertbestimmung für komplizierte Funktion, Grenzwertsätze, Stetigkeit 14:01
• Beispiel für Regel von L'Hôpital 5:06
• null hoch null als Grenzwert; Stetigkeit 12:57
• Grenzwertbetrachtung mit Bruch und Potenzen 6:01
• Grenzwertbetrachtung mit Bruch und Wurzel 9:07
• Grenzwertbetrachtung mit Bruch und Wurzel, anderes Beispiel 7:23
• Grenzwertbetrachtung mit Bruch und Cosinus 2:21
• Grenzwertbetrachtung mit Sinus, Bruch und Potenzen 1:45
• Grenzwertbetrachtung; L'Hospital 5:25
• Exponentialfunktion wächst schneller als jedes Polynom 5:40
• Logarithmus wächst langsamer als jede Wurzel 5:13
• Grenzwert n-te Wurzel aus n 4:38
• Grenzwertbetrachtung rationale Funktion; L'Hospital 2:35
• erfundene Regeln und ein zu knapper Beweis 11:26

---

Vorlesung 5/6 - Grundlagen zu Ableitungen und Integralen

• Skript unter MATERIALIEN

Vorlesung 5:

1. Momentangeschwindigkeit, Ableitung 8:17 
2. Ableitung 11:02 
3. Ableitungsregeln 6:03 
4. Einschub Schreibweise Ableitung 3:23 
5. Kettenregel, Ableitung Exponentialfunktionen, Logarithmus 8:35 
6. Ableitung Potenzen, Wurzeln, Sinus 10:00 
7. weiter Ableitung Sinus 6:27 

Vorlesung 6:

1. Integral, Stammfunktion 10:35 
2. weiter Stammfunktionen 3:02 
3. weiter Stammfunktionen 3:10 
4. bestimmtes Integral 9:25 
5. weiter bestimmtes Integral 7:09

Ergänzungen (optional zum Üben und Vertiefen):

• Kehrwert ableiten 14:31 
• Wurzel ableiten 14:54 
• Faktor-, Summen- und Produktregel der Ableitung 14:04
• Quotientenregel 7:39
• Kettenregel 10:34
• kompliziertere Ableitung 4:28
• Ableitung und Wurfparabel 18:05
• Abstand zweier windschiefer Geraden per Ableitungen 29:07
• Quotientenregel, Kettenregel angewendet 6:35
• Wurzel(52) schätzen, Tangentengerade an Wurzelfunktion 21:32
• Fläche unter Sinus-Halbwelle 5:19
• Strecke aus Geschwindigkeitsverlauf, Integral, Stammfunktion, Einheiten 29:13
• Fläche unter Parabel halbieren, Integral 18:33
• Schwerpunkt der Fläche unter Parabel, Integral 16:05

---

Vorlesung 7 - Ableitung

• Skript unter MATERIALIEN

Vorlesung:

1. Ableitung, Tangente, Sekantensteigung 27:10
2. Ableitung von Summen und Produkten 11:25
3. Kettenregel 19:44
4. Quotientenregel 6:44
5. Ableitung exp, log, Potenz 13:25
6. Ableitung sin, cos, arcsin 11:28

Ergänzungen (optional zum Üben und Vertiefen):

• Fingerübungen zu Ableitungen; Kettenregel, Potenzregel, Produktregel, Quotientenregel 11:58
• Schätzen mit der Ableitung; Tangentengerade 18:59
• Nur bei Exponentialfunktionen ist die Ableitung konstantes Vielfaches der Funktion 8:33
• Ableitung Tangens und Arkustangens 20:18
• Ableitungen, ein paar Fingerübungen 22:36
• zentrale Differenzformeln; Ableitung numerisch 8:12
• senkrechter Wurf; Differentialgleichung 23:42
• Kondensator entladen; Differentialgleichung 14:12

---

Vorlesung 8 - lokale Extrema, Wendepunkte

• Skript unter MATERIALIEN

Vorlesung:

1. lokale, globale Minima, Maxima 15:59
2. lokale Minima und Maxima, Kriterien 14:26
3. Wendepunkte 11:11

Ergänzungen (optional zum Üben und Vertiefen):

• Beispiel lokales Maximum, lokales Minimum 12:59
• Ableitung größer null, streng monoton 7:30
• optimale Dose, maximales Volumen, minimale Oberfläche, Ableitung 35:52
• schnellste Verbindung, Ableitung, snelliussches Brechungsgesetz der Optik 14:32
• Minimum, Maximum eines Polynoms 8:21
• Monotonie mit Ableitung nachweisen 5:01
• Monotonie und Ableitung, Problemfall 5:08
• Wendepunkte Glockenkurve 10:39
• Polynom mit vorgegebenen Wendepunkten 12:57
• Bildgröße, optimaler Standpunkt 13:35

---

Vorlesung 9 - lineare Näherung samt Anwendungen

• Skript unter MATERIALIEN

Vorlesung:

1. Lineare Näherung und ihr Fehler 29:52
2. Numerische Schätzung 1., 2. Ableitung 14:09

Ergänzungen (optional zum Üben und Vertiefen):

• Ableitung von Messreihen schätzen, numerisches Differenzieren, Fehlerschätzung 29:59
• Tangentengerade an sin(x²) 15:56
• ln(3) mit linearer Näherung schätzen 8:29
• Tangentengeraden durch Ursprung an Parabel 9:17
• lineare Näherung für kleine Drehung 18:41
• Linsengleichung auflösen; Fehlerrechnung; lineare Näherung 10:43

---

Vorlesung 10 - Integral

• Skript unter MATERIALIEN

Vorlesung:

1. Idee des Integrals 22:41
2. Stammfunktion, unbestimmtes Integral, Hauptsatz 21:01
3. Uneigentliche Integrale 15:42
4. optional: Numerische Integration, Trapezregel, Simpson-Regel 19:50

Beispiel der Zerlegung eines Intervalls [a,b] in n=8 Teile (Obersumme lila und Untersumme orange)

Ergänzungen (optional zum Üben und Vertiefen):

• Zusammenfassung bestimmtes Integral, Stammfunktion, Wurzelfunktion integrieren 11:51
• Pi mit Integral und Arcustangens berechnen; Leibniz-Reihe 13:08
• numerische Integration, Trapezverfahren, Fehlerschätzung, Romberg, Richardson 22:41
• Integrale mit Sinus und Partialbruchzerlegung 17:41
• Stammfunktion der Betragsfunktion 3:48

---

Vorlesung 11 - Integrationsregeln

• Skript unter MATERIALIEN

Vorlesung:

1. Partielle Integration 17:23
2. Substitutionsregel 13:22
3. Integration durch Partialbruchzerlegung 21:00

Ergänzungen (optional zum Üben und Vertiefen):

• Partielle Integration, Substitutionsregel, Integration durch Partialbruchzerlegung 19:33
• Beispiele partielle Integration, Substitutionsregel, Integration durch Partialbruchzerlegung 37:16
• partielle Integration; Fingerübung 7:34
• partielle Integration; Logarithmus integrieren 2:27
• doppelte partielle Integration; x Quadrat mal Sinus 5:38
• Integration durch Substitution; Fingerübung 8:04
• Integration durch Substitution; weitere Fingerübung 9:04
• drei Wege für Integration durch Substitution 11:27

---

Vorlesung 12 - Schmiegeparabel, Taylor-Polynome

• Skript unter MATERIALIEN

Vorlesung:

1. Tangentengerade, Schmiegeparabel, Taylor-Polynome 14:39
2. Taylor-Polynom für Wurzelfunktion 12:45
3. Taylor-Reihe, Potenzreihen, Teil 1 17:25
4. Taylor-Reihe, Potenzreihen, Teleskopsumme, Teil 2 19:41

Ergänzungen (optional zum Üben und Vertiefen):

• kubische Wurzel mit Schmiegeparabel nähern, Taylor-Polynom 16:21
• nichtlineare Gleichung mit Schmiegeparabel in quadr. Gleichung umwandeln, Taylor 12:14
• Divergenz der harmonischen Reihe mit Integral zeigen 6:56
• Taylor-Näherung für natürlichen Logarithmus 10:25

• Wolfram Alpha: Taylor Reihe für beliebige Funktionen mit graphischer Darstellung
• Approximation von sin(x) durch Taylorpolynome Pn vom Grad 1, 3, 5 und 7:

 

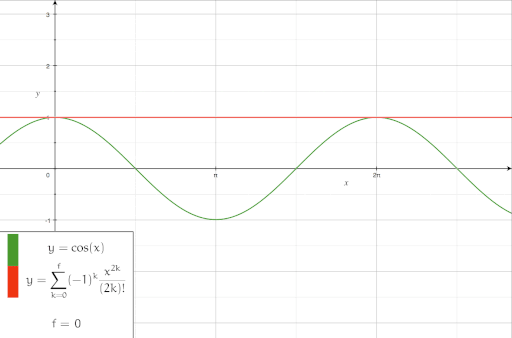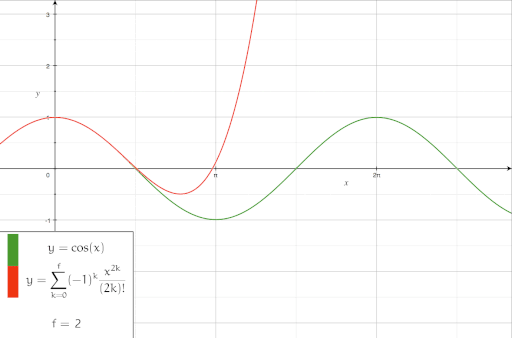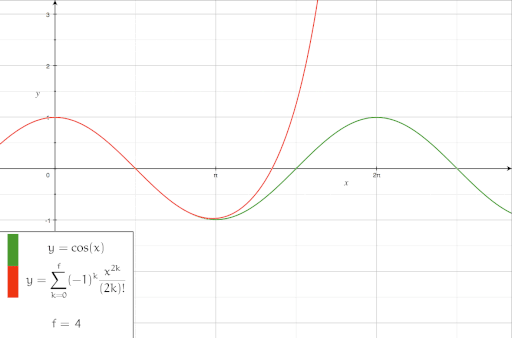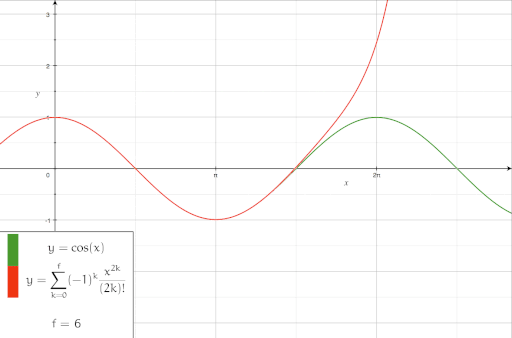
• Die Cosinusfunktion um den Punkt 0 entwickelt, in sukzessiver Näherung:

• Approximation von ln(x) durch Taylorpolynome der Grade 1, 2, 3 bzw. 10 um den Entwicklungspunkt 1. Die Polynome konvergieren nur im Intervall (0, 2]. Der Konvergenzradius ist also 1:

---

Vorlesung 13 - Rest nach Taylor, Potenzreihen

• Skript unter MATERIALIEN

Vorlesung:

1. Taylor-Rest, Teil 1 9:30
2. Taylor-Restformel, Teil 2, Abschätzung des Fehlers 28:46
3. Taylor-Rest, Beispiel für Fehlerschätzung 8:55
4. Potenzreihen, Konvergenzradius, Teil 1 14:54
5. Konvergenzradius, Teil 2 18:07
6. Potenzreihen und Analytische Funktionen 12:32
7. wird nicht behandelt: Differentialgleichungen mit Potenzreihen lösen 12:47

Ergänzungen (optional zum Üben und Vertiefen):

• Potenzreihe für Arcustangens; Konvergenzradius 42:46
• Taylor-Näherung und Fehler für Sinusfunktion 17:20
• Potenzreihe für Logarithmus aus geometrischer Reihe 4:55
• Potenzreihenansatz für Differentialgleichung; Beispiel Taylorpolynom 13:26
• Potenzreihenansatz für Differentialgleichung 19:14
• kubische Wurzel mit Taylorpolynom schätzen; Fehlerschranke 10:34

• Kreiszahl PI mit Taylorreihe von Arcustangens berechnen: arctan(1) = PI / 4
• http://de.wikipedia.org/wiki/Arcus-Tangens#Reihenentwicklung
• http://de.wikipedia.org/wiki/Kreiszahlberechnung_nach_Leibniz
• Mit Java 8 die ersten 1000.000.000 Summanden:

---

Vorlesung 14 - Vektorräume

• Skript unter MATERIALIEN (ab Kapitel 2; nicht alles aus dem Überblick wird bei uns behandelt)
• Zur Wiederholung der grundlegenden Konzepte von Vektoren aus der Schule (oder falls Sie das noch nie gesehen haben) empfehle ich in https://www.bigdev.de/p/mathevorkurs.html die Videos zu Vektoren 067 - 076. 

Vorlesung:

1. optional (nicht alles aus dem Überblick wird bei uns behandelt): Überblick 2. Semester; Lineare Algebra, Differentialgleichungen usw. 40:28
2. Pfeile, Vektoren, gerichtete Größen 17:18
3. Ebene R2 und Raum R3 13:38
4. Vektorraum 16:01
5. Basis, Dimension 20:51

Ergänzungen (optional zum Üben und Vertiefen):

• Vektorraum, Untervektorraum, Basis, Dimension 32:02
• Dimension von Kurven, Flächen; Hausdorff-Dimension; Fraktal, Koch-Kurve 25:30
• Begriff Vektorraum; Vektor aus zwei gegebenen Vektoren bilden 10:29
• Vektorraum der Polynome; Basis 17:04
• Vektorraum der sinusförmigen Schwingungen; Zerlegung in sin und cos 9:26

---

Vorlesung 15 - Geradengleichung, Skalarprodukt

• Skript unter MATERIALIEN

Vorlesung:

1. Geradengleichungen in Parameterform 15:09
2. Länge eines Vektors 10:27
3. Skalarprodukt, Teil 1 10:05
4. Skalarprodukt Teil 2, Orthogonalität 24:49

Ergänzungen (optional zum Üben und Vertiefen):

• Probleme der Geradengleichung mx plus b 9:35
• Abstand Gerade vom Ursprung mit Ableitung und mit Normale 19:35
• Abstand Ebene vom Ursprung, aufwendige Form mit Ableitung 14:51
• Geraden auf Parallelität prüfen 4:25
• Schnittpunkt zweier Geraden 11:27
• Schnittmenge Ebene mit xy-Ebene 3:20
• prüfen, ob Ebene durch Ursprung geht 8:54
• Winkel mittels Skalarprodukt bestimmen 5:33
• Dreieck auf Rechtwinkligkeit prüfen 5:20
• Vektor in yz-Ebene senkrecht zu gegebenem Vektor 7:48
• Geradengleichung in Normalenform 12:09
• Parallelogrammidentität; Diagonalen eines Parallelogramms 9:56
• Winkel zwischen zwei Geraden im R² 5:50

---

Vorlesung 16 - Matrizen

• Skript unter MATERIALIEN

Vorlesung:

1. Matrizen, Transposition, MATLAB(R) 21:59
2. Matrix mal Vektor, Matrix mal Matrix 23:04
3. Skalierung, Drehungsmatrix, Verschiebung 29:40

Ergänzungen (optional zum Üben und Vertiefen):

• Scherungsmatrix 6:16
• Rotation um beliebigen Punkt, affine Abbildung, Verschiebungsvektor, Rotationsmatrix 14:04
• geometrische Wirkung einer Matrix; inverse Matrix 17:54
• Spiegelung und Drehung nacheinander; Matrizenmultiplikation 7:20
• Nichtkommutativität des Matrizenprodukts 9:03
• zwei Spiegelungen nacheinander; Reihenfolge; Matrizenmultiplikation 12:12
• achte Potenz einer Matrix; Matrizen und komplexe Zahlen 8:44
• dritte Potenz einer Matrix ist die Einheitsmatrix 3:30
• Spiegelungsmatrix aus Spiegelungsachse berechnen 11:46
• Spiegelungsachse aus Punkt und Bild bestimmen 5:20
• Matrix für Drehung um Hauptdiagonale im Raum 5:44
• Rezept für Matrizenprodukt 2:33

---

Vorlesung 17/18 - Lineare Gleichungssysteme, Rang, Kern

• Skript unter MATERIALIEN
• Extra-Skript

Vorlesung 17:

1. Playlist (3 Videos): Einführung Lineare Gleichungssysteme 1-3 mit Extra-Skript
2. Bitte meinen Kanal abonnieren und die 🔔 drücken:
   
   
   
   
3. Lineare Gleichungssysteme, Existenz und Eindeutigkeit von Lösungen 14:08
4. Existenz von Lösungen linearer Gleichungssysteme 14:42

Vorlesung 18:

1. Spaltenraum, Bild, Rang einer Matrix 18:50
2. Eindeutigkeit der Lösung, homogenes Gleichungssystem 17:45
3. Kern, Defekt einer Matrix 12:25
4. Zeilenrang, Spaltenrang, unter-, überbestimmt 25:56

Ergänzungen (optional zum Üben und Vertiefen):

• Rang, Spaltenraum, Defekt, Kern einer Matrix, lineares Gleichungssystem 23:05
• Lineare Gleichungssysteme; Lösungen nicht existent oder nicht eindeutig 9:40
• Spaltenraum, Rang, Defekt einer 2x3-Matrix 21:17
• Matrix zu gegebenem Spaltenraum finden 2:46
• Matrix mit Rang 3 mal Matrix mit Rang 1 soll Nullmatrix sein 13:26
• Beispiel Spaltenraum, Bild, Rang, Kern, Defekt; lineares Gleichungssystem 23:03
• weiteres Beispiel Spaltenraum, Bild, Rang, Kern, Defekt; lineares Gleichungssystem 12:11

---

Vorlesung 19/20 - Determinante, Spatprodukt, Vektorprodukt, inverse Matrix

• Skript unter MATERIALIEN

Vorlesung 19:

1. Determinate, Teil 1 14:42
2. Determinante, Teil 2, Parallelepiped 18:25
3. Determinante, Teil 3, antisymmetrische Multilinearform 15:54
4. Determinante, Teil 4, Entwickeln, Sarrus 28:23

Vorlesung 20:

1. Spatprodukt 3:54
2. Vektorprodukt rechnerisch 24:57
3. Vektorprodukt geometrisch 22:45
4. Produkte mit Vektoren, Zusammenfassung 7:14
5. Inverse Matrix 15:18

Ergänzungen (optional zum Üben und Vertiefen):

• Fläche eines Parallelogramms im R³, Vektorprodukt, Kreuzprodukt 8:43
• Vektorprodukt auflösbar oder nicht 3:02
• Trägheitstensor und Drehimpuls mit Vektorprodukt, Spatprodukt, Skalarprodukt 47:22
• Fläche eines Parallelograms im R² mittels Determinante 5:40
• eine 3x3-Determinante ausrechnen 5:06
• eine 4x4-Determinante ausrechnen 14:01
• Fläche eines Dreiecks im Raum 10:26
• Vektorprodukt gleich gegebenem Vektor 4:29
• Gerade senkrecht durch Ebene; Abstand Ebene von Ursprung 13:19
• Vektor senkrecht zu drei gegebenen im R^4 6:25
• doppeltes Vektorprodukt; BAC-CAB-Formel 12:40

---

Vorlesung 21 - Cramer-, Gauss-, Jacobi-Verfahren

• Skript unter MATERIALIEN

Vorlesung:

1. Cramer-Verfahren 16:30
2. Gaußsches Eliminationsverfahren 20:48
3. Jacobi-Verfahren, iterative Lösung 12:45
4. Lineare Gleichungssysteme mit MATLAB(R) und Wolfram Alpha 9:09

Ergänzungen (optional zum Üben und Vertiefen):

• Lineares Gleichungssystem, Gaußsches Eliminationsverfahren, Cramer-Regel, inverse Matrix 26:22
• mit Cramer-Regel 3x3-Matrix invertieren 10:43
• inverse Matrix eines Matrixprodukts 4:45
• inverse Matrix einer 2x2-Matrix; Gleichungssystem lösen 15:45
• vier Lösungsverfahren für lineare Gleichungssysteme; Cramer, Gauß, Jacobi, inverse Matrix 29:15
• Gleichungssystem 2x3; Gaußsches Eliminationsverfahren; Bild, Rang, Kern, Defekt 22:07

---

Vorlesung 22/23 - Eigenvektoren

Vorlesung 22 - Skript unter MATERIALIEN

1. Eigenwerte, Eigenvektoren 11:11
2. Anwendungen von Eigenvektoren 16:51
3. Bestimmung von Eigenwerten 25:45
4. Eigenwerte, Eigenvektoren bestimmen; charakteristisches Polynom 34:21

Vorlesung 23 (ohne Skript - Üben, Üben, Üben!):

1. Eigenwerte, Eigenvektoren symmetrischer Matrizen 10:21
2. Eigenwerte einer 3x3-Matrix 15:07
3. Eigenvektoren von 2x2- und 3x3-Matrizen bestimmen 14:37
4. Matrix zu Eigenvektor und Eigenwert bestimmen 5:22
5. Eigenwerte einer 2x2-Drehungsmatrix 2:03
6. Eigenwerte und Eigenvektoren einer 3x3-Matrix 23:15
7. Eigenwerte mit Spur und Determinante prüfen 8:32
8. Eigenwerte einer 3x3-Matrix; Test mit Spur und Determinante 5:39
9. Eigenvektor zu einer 3x3-Matrix; Eigenwert gegeben 11:36
10. Eigenwerte, Eigenvektoren einer 2x2-Matrix 9:06

---

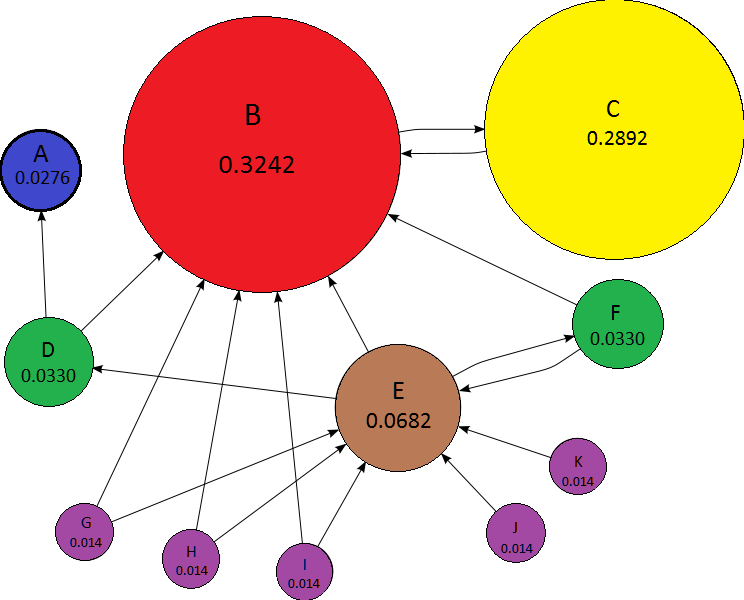
Vorlesung 24 - Anwendung von EV: Google Page Rank

Lesen Sie vorab die Artikel:

• Google's PageRank-Algorithmus zur Bewertung von Webseiten für Suchmaschinen: 
• Wikipedia, 
• zum Schmökern (optional): Original-Paper der Google-Gründer Larry Page und Sergey Brin
• Markov-Ketten und stochastische Matrizen: Wikipedia

„PageRank-Beispiel“ von Zetkin - Eigenes Werk. Lizenziert unter CC BY-SA 3.0 über Wikimedia Commons.

Weiterführend und weitere Anwendungen in der Informatik: https://www.coursera.org/course/matrix

---